Урок 8

Растровое изображение линии - всё из точки! Алгоритм Брезенхема как основа основ.


Версия игры, реализованная в предыдущих уроках, выводит графику "псевдоспрайтами" - ASCII-символами. Есть вполне успешные игры игры, основанные на подобном виде графики - например Dwarf Fortress - хотя, конечно, в 70-x, да и в 80-х годах прошлого века таких игр было несравненно больше, даже сам тетрис - изначально был создан c выводом графики символами алфавита, фигурки тетриса составлялись из буквы "Ш". Cуществовало и множество текстовых игр - но если текстовые игры не завязаны на особенности вывода изображения, и играть в них можно, к примеру, с использованием голосового синтезатора вместо монитора, игры с ASCII-графикой буквами именно отрисовывают картинку.

В ходе развития компьютерных игр появлялось множество различных вариантов отрисовки графики игр, главенствующим на насколько десятилетий закрепилась спрайтовая графика. Спрайтовая графика отличается от ASCII-графики тем, что ASCII использует набор символов: неизменных, не всегда подходящих и - зависящих от устройства вывода. Зачастую у игры нет возможности задать устройству вывода цвет, соотношение высоты буквы к её ширине, к примеру, и даже нет возможности проверить что все символы будут одинаковой ширины - а попытка вывести картинку символами различной ширины картинку разрушит непоправимо. Спрайтовая же графика позволяет контролировать спрайт (при условии, что пиксель на мониторе "квадратный", с шириной равной высоте - а это практически стандарт уже очень давно, и если на самом экране это вдруг не так - то само устройство вывода берет на себя заботу, чтобы изображение сохраняло правильные пропорции). Спрайты более приспособлены для создания двухмерных игр - и во времена расцвета спрайтовых игр компьютеры с большим трудом (трудом программистов, естественно) ещё могли обрабатывать трёхмерные миры. С развитием компьютеров и технологий компьютерной графики появлялось всё больше трёхмерных игр - довольно быстро основным способом построения трёхмерной графики стало составление изображений из полигонов-треугольников (хотя существовали и существуют другие подходы).

Но запрос на создание трёхмерных игр уже как минимум в 1974 году привёл к появлению игр MazeWar (псевдо-3D) и Spasim (полноценная трёхмерная игра). Трёхмерное изображение в Spasim (и в MazeWar, частично) отображается с помощью двухмерных отрезков. Сейчас в современных играх изображения составляются почти так же, на основании треугольных полигонов. Треугольный полигон - это просто закрашенный треугольник. Треугольник в современных играх отрисовывается заполненным, но в первых трёхмерных играх полигоны отрисовывались полыми, с видимыми гранями - и невидимыми поверхностями. Закрасить треугольник сложнее, чем нарисовать только линию, а грани треугольника и являются именно отрезками. Так что для создания трёхмерной игры в первую очередь стоит начать с вывода на экран отрезков.

Для отрисовки линий на графопостроителях (устройства вывода изображения на бумаге, наносящие изображения не точками - растром, как мы привыкли, а рисующие их линиями) был предложен очень эффективный по нагрузке на вычислительное устройство алгоритм Брезенхема. С готовым алгоритмом можно ознакомиться внизу урока, в течение урока показано, как можно прийти от наивной реализации к эффективной отрисовке линии с помощью Брезенхема. Для создания современных игр алгоритм не нужен вообще, так как отрисовкой треугольников (и линий) занимается видеокарта. Но пока что игра пишется с так называемым софтовым рендером, работающем на процессоре, а не на видеокарте - и все графические операции для которого предстоит реализовать самостоятельно.

В третьем уроке уже осуществлялась отрисовка линии, для этого не было выделено отдельной функции и отрисовка происходила непосредственно в main():

for (int x = 1; x < WIDTH - 1; x++) { int y = HEIGHT * x / WIDTH; int x_tmp = (x + t / DAMPING) % WIDTH; draw_pixel(x_tmp, y, '#'); }
Переменная t (как и введённая для её адаптации переменная x_tmp), использована для анимации, но отрисовка линии не должна задумываться о анимации - это задача вызывающего отрисовку кода, так что остаётся:
for (int x = 1; x < WIDTH - 1; x++) { int y = HEIGHT * x / WIDTH; draw_pixel(x, y, '#'); }
Этот код не сильно подходит для рисования линий в общем случае, но лиха беда начало - можно начать улучшать функцию до удовлетворительного результата итеративно:
main.c
int main_cycle = 0;		/* stop program if 0 */
int t = 0;

void init_graphics();
void draw_background();
void render_scene();
void finalize_graphics();
void finalize_world();
void draw_line(int x1, int y1, int x2, int y2, char sprite);

void quit_game(int dummy)
{
    main_cycle = 0;
}

void init_player_input(void (*f)());

int main()
{
    init_graphics();
    init_player_input(quit_game);

    main_cycle = 1;             /* Initializing runprogram flag */

    draw_background();
    draw_line(10, 1, 70, 5, '*');
    render_scene();

    while(main_cycle)
    {
        ;
    }

    finalize_graphics();

    return 0;
}
graphics.c
...

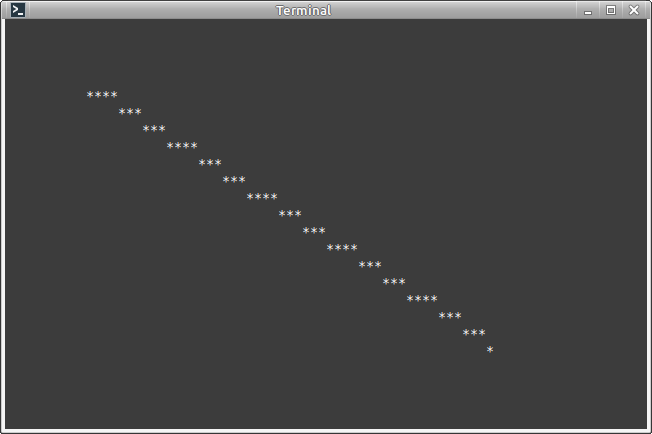
void draw_line(int x1, int y1, int x2, int y2, char sprite)
{
    for (int x = x1; x + x1 <= x2; x++)
    {
        int y = HEIGHT * x / WIDTH + y1;
        draw_pixel(x, y, sprite);
    }
}

...
Функция работает. Ну работает же? Есть куча проблем, но даже чтобы начать их исправлять стоит добавить символы начала и конца линии - для визуального контроля точности построения (иксы отрисовываются до начала построения линии, и если они после вывода линии остались видны - значит линия построена неверно):
draw_line():
draw_pixel(x1, y1, 'X');
draw_pixel(x2, y2, 'X');

for (int x = x1; x + x1 <= x2; x++)
{
    int y = HEIGHT * x / WIDTH + y1;
    draw_pixel(x, y, sprite);
}
...Мимо.

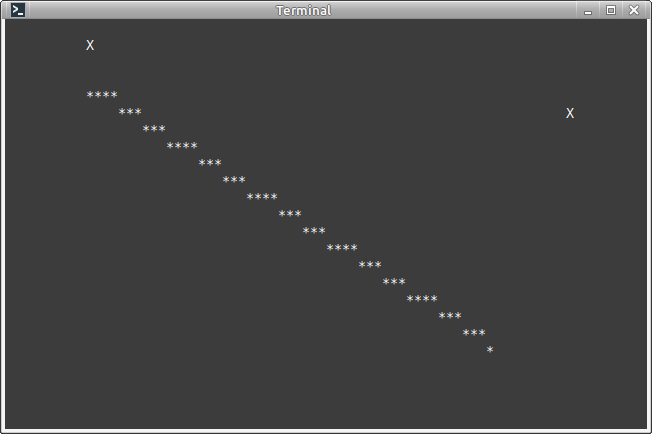
x пробегает от x1 до x2, но изменение y зависит не от конечного положения отрезка, а от соотношения ширины и высоты экрана - тяжелое наследие старого кода. Стоит высчитывать позицию y на каждом шаге:
draw_line():
...

for (int x = 0; x + x1 <= x2; x++)
{
    int y = (y2 - y1) / (x2 - x1) * x;
    draw_pixel(x + x1, y + y1, sprite);
}
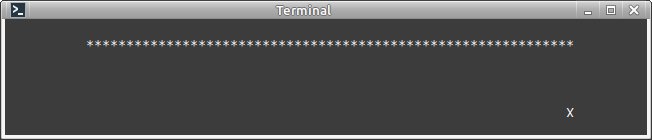
Какие проблемы есть в строке int y = (y2 - y1) / (x2 - x1) * x (ну, кроме очевидного деления на ноль)?
Проблема в целочисленном делении. В самой формуле (dy / dx) * x проблем нет, но результат деления при 0 < dx < dy будет менее 1: 0 < dx / dy < 1. При целочисленном делении /, соответственно, результат в таком случае округляется вниз и получается равен нулю. Решение простое - выполнять умножение до целочисленного деления (информация теряется на делении, выполнение деления последним позволяет исключать попытку использования утерянной информации в расчётах): int y = x * (y2 - y1) / (x2 - x1):
draw_line():
...

for (int x = 0; x + x1 <= x2; x++)
{
    int y = x * (y2 - y1) / (x2 - x1);
    draw_pixel(x + x1, y + y1, sprite);
}
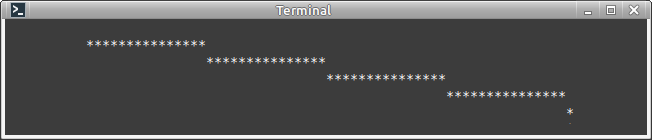
Линия следует из точки в точку, но делает это как-бы "сверху" - если приложить к центрам крайних символов линейку, линия будет всегда над линейкой. Соответственно, линия отображается неверно (доказательство не формальное, зато наглядное). Опустить линию на один пиксель (на один символ, слово pixel складывается из словосочетания picture element, и изображение линии складывается из символов - пикселей) не поможет - тогда отображённая линия станет точно так же "ниже" прямой между центрами. Чтобы линия находилась в равной мере над и под осью между иксами - нужно сдвинуть её влево, причём ровно на половину длины одной горизонтальной ступени.
Длина горизонтальной ступени - это длина линии по X, делённая на количество ступеней - высоту линии по Y. Соответственно смещение линии будет равно половине этой величины: 
int offset = (x2 - x1) / (y2 - y1);
offset = offset / 2;
Вернее, для исключения потери точности на двух делениях: 
int offset = (x2 - x1) / ((y2 - y1) * 2);

Простое решение - сдвинуть каждый пиксель изображения на величину offset не сработает:

draw_line():
...

for (int x = 0; x + x1 <= x2; x++)
{
    int offset = (x2 - x1) / ((y2 - y1) * 2);
    int y = x * (y2 - y1) / (x2 - x1);
    draw_pixel(x + x1 - offset, y + y1, sprite);
}

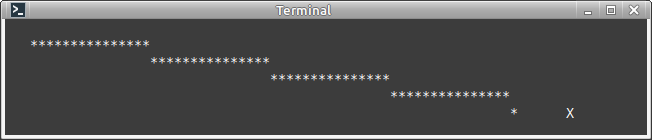
Сдвигать координату x не нужно, нужно сдвигать только y по вертикали так, как будто x сдвинут - в расчёте y учитывать "сдвинутое" значение x, но для отрисовки использовать несдивинутую горизонтальную координату:

draw_line():
...

for (int x = 0; x + x1 <= x2; x++)
{
    int offset = (x2 - x1) / ((y2 - y1) * 2);
    int y = (x + offset) * (y2 - y1) / (x2 - x1);
    draw_pixel(x + x1, y + y1, sprite);
}

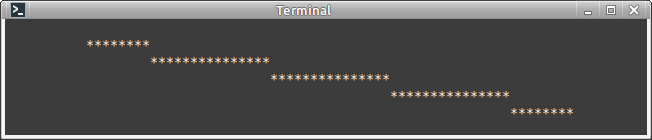
Визуально картинка соответсвует ожиданиям! Но внимание должно цепляться за две операции деления, причём одну из них можно (и нужно!) вынести из цикла:

draw_line():
...

int offset = (x2 - x1) / ((y2 - y1) * 2);

for (int x = 0; x + x1 <= x2; x++)
{
    int y = (x + offset) * (y2 - y1) / (x2 - x1);
    draw_pixel(x + x1, y + y1, sprite);
}
Другая же операция деления участвует в вычислении значения координаты Y, и переменная, в вычислении которой участвует это деление, должна обновляться на каждом шаге цикла. Для каждого кадра изображения, для каждой линии на экране, для каждого пикселя каждой линии каждого кадра будет выполняться операция деления - таких пикселей может быть и больше, чем пикселей на экране, так как линии могут перекрывать друг друга.
Чтобы исключить лишние деления можно, в первую очередь, заметить, что деление используется для подсчёта смещения по горизонтали на каждом шаге - и каждый шаг смещение увеличивается на одинаковую величину. Но так как эта "одинаковая величина" получается меньше единицы, её можно расчитать заранее только в вещественных числах - и cохранить значение изменения нужно в переменной с плавающей точкой. В начале урока уже приводилась ситуация, когда целочисленное смещение, меньшее единицы - просто округлялось до нуля, и никакого смещения линии не происходило. Так что при расчёте смещения по вертикали нужно не забывать про накапливающуюся дробную часть числа - пусть и отбрасываемую при присваивании целочисленной переменной y. А саму величину смещения на шаг dy нужно объявить переменной с плавающей точкой:
draw_line():
...

int offset = (x2 - x1) / ((y2 - y1) * 2);
float dy = (float)(y2 - y1) / (float)(x2 - x1);

for (int x = 0; x + x1 <= x2; x++)
{
    int y = (x + offset) * dy;
    draw_pixel(x + x1, y + y1, sprite);
}
Код избавился от множественного деления, но взамен получил множественное умножение с плавающей точкой. Всё же операции с плавающей точкой - которых раньше не было - могут выполняються дольше, чем операции над целыми числами. В современных процессорах это не обязательно должно быть так (засчёт потери точности деление с плавающей точкой - то есть, по сути, замена умножения и деления сложением и вычитанием экспонент чисел. в каких-нибудь новых процессорных инструкциях в принципе может обогнать старое-доброе обычное целочисленное деление). Но (по историческим причинам) все операции с плавающей точкой выполняются отдельным набором команд. Раньше ими занимался "математический сопроцессор", который, хоть и мог быть расположен в одном корпусе с процессором (а мог - и не быть), но всё же являлся отдельным процессором. Соответсвенно при необходимости выполнить операцию над числом с плавающей точкой (из-за особенностей архитектуры) - нужно было кроме самого вычисления (которое тоже занимает время, т.е. количество процессорных тактов) ещё запустить отдельную программу сопроцессора, передать ей управление, подготовить для сопроцессора данные, дождаться результата, данные забрать - и забрать управление программой. Сейчас деление далеко не обязано использовать такой подход, но в общем, чем реже используются переменные с плавающей точкой, тем быстрее.

Число с плавающей точкой используется для переменной dy потому, что в переменной y накапливается смещение - каждый шаг в дробную, отбрасываемую часть вычисления x * dy добавляется смещение dy, пока не сменится целая часть. Как дробная часть достигнет максимума, целая часть сменится и произойдёт переход на следующую строку. В предыдущем варианте функции дробная, отбрасываемая часть y неявно используется как аккумулятор ошибки, целая же часть - считает, сколько раз аккумулятор был переполнен. Можно периписать код так, чтобы аккумулятор был указан явно. Смысл нового варианта функции не столько в явном указании величины накопления ошибки, а избавление от умножения с плавающей точкой - замена умножения на сложение, так как цикл пробегает все значения x от 0 до x2-x1, все значения можно получить не умножением dy на 0, 1, 2 и т.д., а просто последовательно прибавлять dy. Такой вариант функции хоть и повышает быстродействие - сложение всё же быстрее умножения, но не избавляет тем не менее пока что от вычислений с использованием вещественных чисел:

draw_line():
...

int offset = (x2 - x1) / ((y2 - y1) * 2);
float dy = (float)(y2 - y1) / (float)(x2 - x1);
float y = offset * dy;

for (int x = 0; x + x1 <= x2; x++, y += dy)
{
    draw_pixel(x + x1, y + y1, sprite);
}
Или то же самое только чуть-чуть с более явной инкрементацией y:
draw_line():
...

int offset = (x2 - x1) / ((y2 - y1) * 2);
float dy = (float)(y2 - y1) / (float)(x2 - x1);
float y = offset * dy;

for (int x = 0; x + x1 <= x2; x++)
{
    draw_pixel(x + x1, y + y1, sprite);
    y += dy;
}
При этом накопление смещения по вертикали на каждом x-шаге было числом с плавающей точкой, что неудовлетворительно по изложенным выше соображениям быстродействия. В идеале линию нужно рисовать пользуясь только целые числа. И без деления. И без умножения. Для всего этого нужно заменить неявное условие смены ряда (шаг по y) по превышению неявного лимита дробной части на явное значение лимита. Сначала просто обозначение концепции:
draw_line():
...

int offset = (x2 - x1) / ((y2 - y1) * 2);
float dy = (float)(y2 - y1) / (float)(x2 - x1);

int y_integer_part = offset * dy;
float y_fractional_part = offset * dy;

for (int x = 0; x + x1 <= x2; x++)
{
    draw_pixel(x + x1, y_integer_part + y1, sprite);

    y_fractional_part += dy;
    if (y_fractional_part > 1.0)
    {
        y_fractional_part -= 1.0;
        y_integer_part++;
    }
}
или то же самое, но с явным вынесением лимита в переменную:
draw_line():
...

int offset = (x2 - x1) / ((y2 - y1) * 2);
float dy = (float)(y2 - y1) / (float)(x2 - x1);
float y_fraction_limit = 1.0;

int y_integer_part = offset * dy;
float y_fractional_part = offset * dy;

for (int x = 0; x + x1 <= x2; x++)
{
    draw_pixel(x + x1, y_integer_part + y1, sprite);

    y_fractional_part += dy;
    if (y_fractional_part > y_fraction_limit)
    {
        y_fractional_part -= y_fraction_limit;
        y_integer_part++;
    }
}

Теперь можно заметить, что значение переменной offset используется только для вычисления значения выражения offset * dy. Это выражение, с учётом выражений, используемых для используемых переменных, можно расписать:

y = x2 - x1 y2 - y1 ⋅ y2 - y1 x2 - x1 ⋅ 1 2
Таким образом значение выражения offset * dy оказывается равно просто 0.5. Эта "половина" - половина от значения лимита, тогда y_fractional_part = y_fraction_limit / 2. В результате же присваивания вещественного значения 0.5 целочисленной переменной y_integer_part вещественное значение округляется вниз, и в переменной оказывается просто 0. Переменная offset в результате упрощения более не нужна:

draw_line():
...

float dy = (float)(y2 - y1) / (float)(x2 - x1);

float y_fraction_limit = 1.0;
int y_integer_part = 0;
float y_fractional_part = y_fraction_limit / 2;

for (int x = 0; x + x1 <= x2; x++)
{
    draw_pixel(x + x1, y_integer_part + y1, sprite);

    y_fractional_part += dy;
    if (y_fractional_part > y_fraction_limit)
    {
        y_fractional_part -= y_fraction_limit;
        y_integer_part++;
    }
}
Каждые несколько шагов по x происходит один переход по y. Для избавления от переменных с плавающей точкой нужно найти способ определить величину dy(доля смещения по вертикали), которая накапливается в y_fractional_part для "перескока" на следующую строку, в целых числах.
Но величина dy обзавелась дробной частью в результате деления на x2-x1. То есть, если умножить на x2-x1 как dy, так и limit - система не изменится, но dy и y_fractional_part перестанут иметь дробную часть:
draw_line():
...

float dy = y2 - y1;

float y_fraction_limit = x2 - x1;
int y_integer_part = 0;
float y_fractional_part = y_fraction_limit / 2;

for (int x = 0; x + x1 <= x2; x++)
{
    draw_pixel(x + x1, y_integer_part + y1, sprite);

    y_fractional_part += dy;
    if (y_fractional_part > y_fraction_limit)
    {
        y_fractional_part -= y_fraction_limit;
        y_integer_part++;
    }
}

Теперь переменные с плавающего типа можно преобразоватьв целочисленные переменные:

draw_line():
...

int dy = y2 - y1;

int y_fraction_limit = x2 - x1;
int y_integer_part = 0;
int y_fractional_part = y_fraction_limit / 2;

for (int x = 0; x + x1 <= x2; x++)
{
    draw_pixel(x + x1, y_integer_part + y1, sprite);

    y_fractional_part += dy;
    if (y_fractional_part > y_fraction_limit)
    {
        y_fractional_part -= y_fraction_limit;
        y_integer_part++;
    }
}
В функции рисования линии остались лишь элементарные операции сложения и вычитания, и только над переменными целочисленного типа. Единственная операция деления на два, можно надеяться, будет преобразована компилятором из деления в битовый сдвиг двоичного числа - действие, которое выполняется элементарно.

Так же (для упрощения читаемости кода) можно заметить, что значения переменных x и y всегда используются в паре с начальными координатами отрезка - и значит могут быть проинициализированы не нулями, а началом отрезка.

draw_line():
...

int dy = y2 - y1;

int y_fraction_limit = x2 - x1;
int y_integer_part = y1;
int y_fractional_part = y_fraction_limit / 2;

for (int x = x1; x <= x2; x++)
{
    draw_pixel(x, y_integer_part, sprite);

    y_fractional_part += dy;
    if (y_fractional_part > y_fraction_limit)
    {
        y_fractional_part -= y_fraction_limit;
        y_integer_part++;
    }
}
Или, ещё проще - вместо отдельных переменных для прохождения всех координат от начала до конца (y_integer_part и x) можно использовать параметры y1 и x1 непосредственно. Переменная y_fractiona_part в классической реализации алгоритма Брезенхема называется error, переменная dy - delta_error, а переменная y_fraction_limit носит название delta_x так как, по сути, является просто изменением координаты X линии:
draw_line():
...

int delta_error = y2 - y1;

int delta_x = x2 - x1;
int error = delta_x / 2;

for (; x1 <= x2; x1++)
{
    draw_pixel(x1, y1, sprite);

    error += delta_error;
    if (error > delta_x)
    {
        error -= delta_x;
        y1++;
    }
}

Теперь последнее оставшееся деление. Оно, хоть и будет соптимизировано компилятором (почти наверняка!), но всё же оно несёт с собой проблему потери точности. Так, для разных значений delta_x, к примеру 2 и 3, значение error будет одинаковым - 1. Переменная error используется для сравнения с величиний delta_x, и инкрементируется (или декрементируется) переменными delta_x и delta_y. Значит, для избавления от деления на 2 можно вместо этого использовать удвоенное значение error, равное просто delta_x, не делённое на 2, и взаимодействовать с error с помощью увеличенных в два раза delta_x и delta_y
Заодно можно заметить, что после использования для итерирования непосредственно параметра x1 вместо переменной x - цикл for() можно заменить на цикл while() (и вынести итерирование x1++ в явном виде из условия цикла). Ещё - не значимый сейчас момент, но в будущем пригодится перенос инкремента error после if(). В таком случае меняется и инициализирующее значение переменной, чтобы компенсировать первый инкремент:

draw_line():
...

int delta_error = y2 - y1;

int delta_x = x2 - x1;
int error = delta_x + delta_error * 2;

while(x1 <= x2)
{
    draw_pixel(x1, y1, sprite);

    if (error > delta_x * 2)
    {
        error -= delta_x * 2;
        y1++;
    }
    error += delta_error * 2;
    x1++;
}

Функция работает в предположении, что начальная координата отрезка не больше конечной, (слева направо), а проекция отрезка на ось ординат меньше, чем проекция на ось абсцисс (линия полога). В общем случае это конечно же не так, и функция должна уметь отрисовывать отрезок между двумя любыми точками:

main.c
...

int main()
{
    int x = 19;
    int y = 2;
    init_graphics();
    init_player_input(quit_game);

    t = 1;
    main_cycle = 1;             /* Initializing runprogram flag */
    /* Main cycle */
    while(main_cycle)
    {
        draw_line(x, y, 00, 00, '1');
        draw_line(x, y, 19, 00, '2');
        draw_line(x, y, 39, 00, '3');
        draw_line(x, y, 59, 00, '4');
        draw_line(x, y, 79, 00, '5');
        draw_line(x, y, 79, 12, '6');
        draw_line(x, y, 79, 23, '7');
        draw_line(x, y, 59, 23, '8');
        draw_line(x, y, 39, 23, '9');
        draw_line(x, y, 19, 23, 'a');
        draw_line(x, y, 00, 23, 'b');
        draw_line(x, y, 00, 13, 'c');
        draw_line(x, y, 00, 03, 'd');
        render_scene();
        t++;
    }

    finalize_graphics();

    return 0;
}

Для корректной отрисовки всех секторов можно отзеркалить все варианты направления линии. Сейчас отрезок рисуется только в четвёртой четверти и только если он пологий. Для отрисовки крутой линии в четвёртой четверти нужно итерироваться не по X, а по Y. Тогда остальные четверти можно отрисовывать либо разменивая начальные точки постороения, либо меня направление обхода отрезка из начальной точки. Для возможности итерироваться по Y стоит заметить, что delta_x и delta_error по сути несут одну и ту же функцию - проекция отрезка на абсцисс и на ординат. Тогда для симметрии стоит переименовать delta_error в delta_y. (И спрятать, заодно, умножения в определения переменных)

draw_line():
draw_pixel(x1, y1, 'X');
draw_pixel(x2, y2, 'X');

int delta_x = x2 - x1;
int delta_y = y2 - y1;
int error = delta_x + delta_y * 2;

delta_x *= 2;
delta_y *= 2;
while(x1 <= x2)
{
    draw_pixel(x1, y1, sprite);

    if (error > delta_x)
    {
        error -= delta_x;
        y1++;
    }
    error += delta_y;
    x1++;
}

Теперь в функции draw_line() можно реализовать два случая: для варианта, когда длина отрезка по X больше длины по Y, и для парного случая:

draw_line():
draw_pixel(x1, y1, 'X');
draw_pixel(x2, y2, 'X');

int delta_x = x2 - x1;
int delta_y = y2 - y1;

if (delta_x > delta_y)
{
    int error = delta_x + 2 * delta_y;
    delta_x *= 2;
    delta_y *= 2;
    while(x1 <= x2)
    {
        draw_pixel(x1, y1, sprite);
        
        if (error > delta_x)
        {
            error -= delta_x;
            y1++;
        }
        error += delta_y;
        x1++;
    }
}
else
{
    int error = delta_y + 2 * delta_x;
    delta_x *= 2;
    delta_y *= 2;
    while(y1 <= y2)
    {
        draw_pixel(x1, y1, sprite);

        if (error > delta_y)
        {
            error -= delta_y;
            x1++;
        }
        error += delta_x;
        y1++;
    }
}
Дублирование кода - налицо)
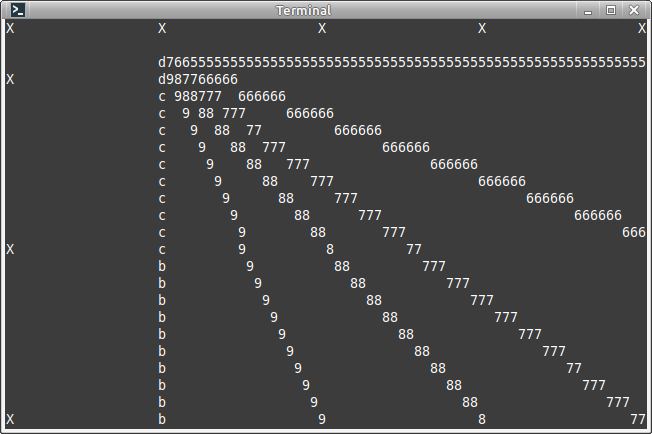
Для избавления от дублирования сначал абсолютно то же самое, чуть перегруппировав операторы внутри блоков пологости\крутизны:
draw_line():
draw_pixel(x1, y1, 'X');
draw_pixel(x2, y2, 'X');

int delta_x = x2 - x1;
int delta_y = y2 - y1;

int error;
if (delta_x > delta_y)
{
    error = delta_x + 2 * delta_y;
}
else
{
    error = delta_y + 2 * delta_x;
}

delta_x *= 2;
delta_y *= 2;
while(x1 <= x2 && y1 <= y2)
{
    draw_pixel(x1, y1, sprite);
    
    if (delta_x > delta_y)
    {
        if (error > delta_x)
        {
            error -= delta_x;
            y1++;
        }
        error += delta_y;
        x1++;
    }
    else
    {
        if (error > delta_y)
        {
            error -= delta_y;
            x1++;
        }
        error += delta_x;
        y1++;
    }
}

В обоих вариантах ветки if происходит по сути одно и то же, но - иксы и игреки меняются местами. Немного подумав, можно придумать хитрый вариант, когда для X и для Y переменная error будет меняться в разных направлениях по числовой оси:

draw_line():
...

if (delta_x > delta_y)
{
    error = 3 * delta_x - 2 * delta_y;
}
else
{
    error = -3 * delta_y + 2 * delta_x;
}

delta_x *= 2;
delta_y *= 2;
while(x1 <= x2 && y1 <= y2)
{
    draw_pixel(x1, y1, sprite);
    
    if (delta_x > delta_y)
    {
        if (error < delta_x)
        {
            error += delta_x;
            y1++;
        }
        error -= delta_y;
        x1++;
    }
    else
    {
        if (error > -delta_y)
        {
            error -= delta_y;
            x1++;
        }
        error += delta_x;
        y1++;
    }
}

Сделан этот небольшой трюк с разным направлением изменения error сделан для того, чтобы две ветки if объединить весьма элегантным образом:

draw_line():
...

while(x1 <= x2 && y1 <= y2)
{
    draw_pixel(x1, y1, sprite);
    
    int error_tmp = error;
    if (error_tmp < delta_x)
    {
        error += delta_x;
        y1++;
    }
        if (error_tmp > -delta_y)
    {
        error -= delta_y;
        x1++;
    }
}
Не очень аккруатная конструкция 3 * delta_x - 2 * delta_y, или, что то же самое, delta_x + 2 * (delta_x - delta_y) появилась оттого, что при манипуляции с избавлением от деления удваивались значения delta_x и delta_x. При этом переменные всё время используются в "удвоенном" значении, а "половинное" значение нужно только для инициализации переменной error . Можно избавиться от "удвоенных" дельт (и сравнивать, соответсвенно, с удвоенным значением error).
draw_line()
...

int error;
if (delta_x > delta_y)
{
    error = delta_x - delta_y;
}
else
{
    error = -delta_y + delta_x;
}

while(x1 <= x2 && y1 <= y2)
{
    draw_pixel(x1, y1, sprite);
    
    int error_tmp = error * 2;
    if (error_tmp < delta_x)
    {
        error += delta_x;
        y1++;
    }
    if (error_tmp > -delta_y)
    {
        error -= delta_y;
        x1++;
    }
}
И теперь error может быть проинициализирована вот так вот просто:
draw_line():
...

int error = delta_x - delta_y;

...

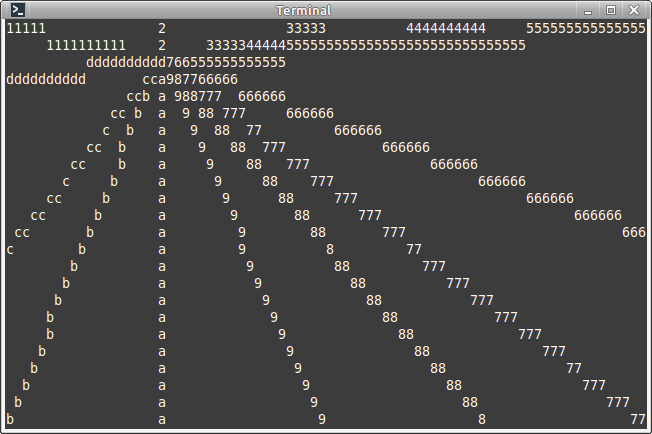
Теперь функция может отрисовывать корректно любую линию из четвёртого квадранта, и отрисовывать любой другой квадрант можно просто меняя направление инкрементации x и y. При этом, правда, нужно будет ещё и изменить условие окончания цикла:

graphics.c
...

void draw_line(int x1, int y1, int x2, int y2, char sprite)
{
    int sign_x = x2 > x1 ? 1 : -1;
    int delta_x = (x2 - x1) * sign_x;

    int sign_y = y2 > y1 ? 1 : -1;
    int delta_y = (y2 - y1) * sign_y;

    int error = delta_x - delta_y;

    while(x1 != x2 || y1 != y2)
    {
        draw_pixel(x1, y1, sprite);
        
        int error_tmp = error * 2;
        if (error_tmp < delta_x)
        {
            error += delta_x;
            y1 += sign_y;
        }
        if (error_tmp > -delta_y)
        {
            error -= delta_y;
            x1 += sign_x;
        }
    }
    draw_pixel(x2, y2, sprite);
}

...
main.c
...

void init_screen();

float fake_sin(int x)
{
    int sign = 1;
    x %= 360;
    if (x > 180)
    {
        sign = -1;
        x = 360 - x;
    }
    float numerator = 4 * x * (180 - x);
    float denominator = 40500 - x * (180 - x);
    return sign * numerator / denominator; 
}


int main()
{
    int x = 0;
    int y = 0;
    init_graphics();
    init_player_input(quit_game);
    
    t = 1;
    main_cycle = 1;        /* Initializing runprogram flag */
    /* Main cycle */
    while(main_cycle)
    {
        x = 1 + 39 * (1 + fake_sin(t / 300 + 0 ));
        y = 1 + 11 * (1 + fake_sin(t / 300 + 90));
        init_screen();
        draw_line(x, y, 00, 00, '1');
        draw_line(x, y, 19, 00, '2');
        draw_line(x, y, 39, 00, '3');
        draw_line(x, y, 59, 00, '4');
        draw_line(x, y, 79, 00, '5');
        draw_line(x, y, 79, 12, '6');
        draw_line(x, y, 79, 23, '7');
        draw_line(x, y, 59, 23, '8');
        draw_line(x, y, 39, 23, '9');
        draw_line(x, y, 19, 23, 'a');
        draw_line(x, y, 00, 23, 'b');
        draw_line(x, y, 00, 13, 'c');
        draw_line(x, y, 00, 03, 'd');
        render_scene();
        t++;
    }

    finalize_graphics();

    return 0;
}

Самостоятельная работа:
  • Растеризация. Почему без неё никак, и как можно бы было без неё?
  • В чём проблема алгоритма Брезенхема? Anti-Aliasing.
  • История появления видеокарт. Зачем? Отличие видеокарты от видеоадаптера.